Balancing binary search trees
Note: I have done very little research on this, faux-balanced is not a technical term, and there is a good chance that this is not an operation you would find on wikipedia. Look up "left rotation" and "right rotation" to do your own research.One of the most versatile data types out there is the binary search tree. It allows you to search, create, or delete item in (ideally) O(log n) time. In order to explain how it works though, we first have to talk about binary search.
If I pick a number between 1 and 1000, while only telling you higher or lower for each of the guesses, how would you play?
You seem to have javascript disabled. It's ok, I still love you :)
I spent an embarassingly long time writing the javascript to make that game happen. I even took extra care in releasing it under the GPL v 3.0. for the 3 people who use LibreJS.
Anyways, the ideal strategy is (obviously) not to go through every single number. The ideal strategy is to remove half the numbers in every guess by just guessing the middle. For example, if your first guess is 500, and my fantastic code response "higher", then you've just eliminated 500 numbers. After that, you can 750 to eliminate 250 numbers, and so on. Using this strategy you can find the answer in 9 or 10 guesses every time, which is far better than doing it in 1000.
Now imagine that instead of trying to find a number, you're trying to find where something is in a sorted list. The same principle applies. Since you know the list is sorted, by checking the middle element you can eliminate half the possible positions for the item you're searching for. This algorithm to search for something by splitting the list in 2 and eliminating one of the halves is called binary search.
Binary search does have the caveat that you can't add something in the middle of the list.
0 1 2 4 5 6 0 1 2 3 4 5 6 As you can see from my crude imagery, in order to add the 3 to this sorted list, the 4, 5, and 6 all had to shift over to the right. This takes time, time which we don't have. We've lost the ability to just add things to the end of our list thanks to our insistence on sorting. What if there was some way to get the blazing efficiency of binary search, but the dynamicallity of just a regular old array.
Introducing binary search trees! Just store the middle element, and the 2 elements to the left and the right.
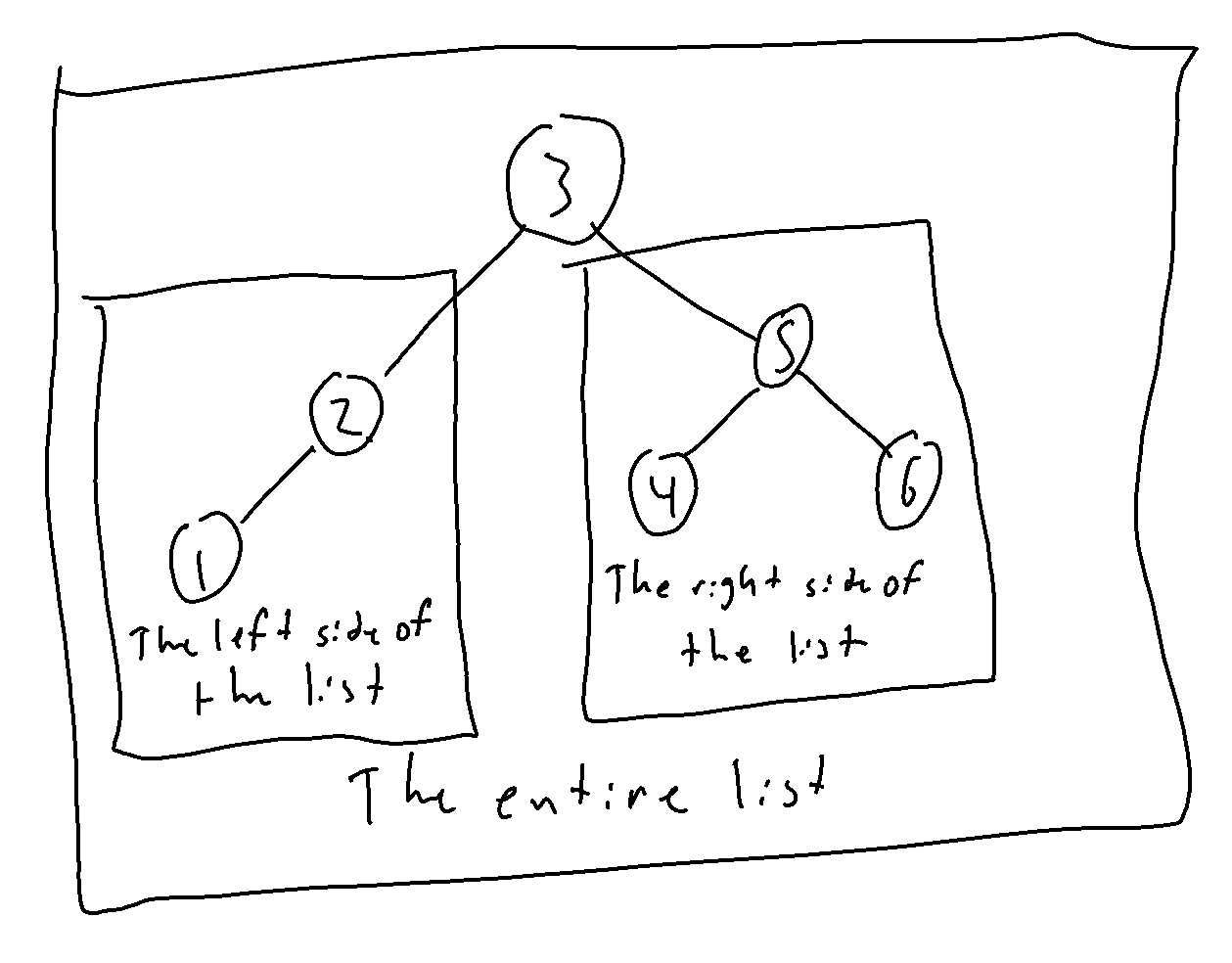
To insert an element, just find out where it should go, and put it there! Just one problem though, these trees aren't always balanced!
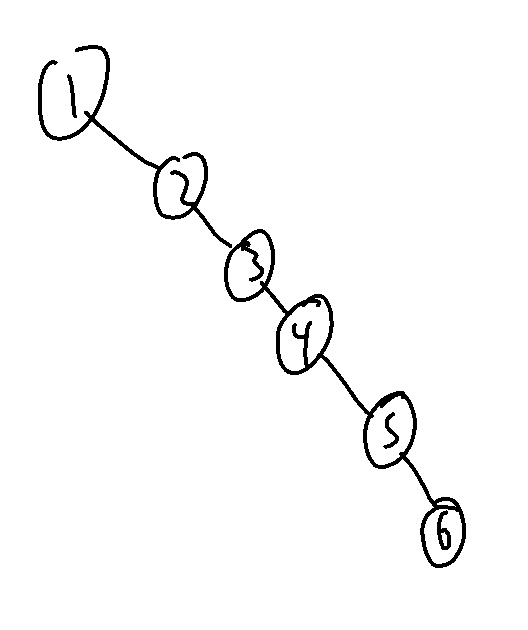
If only there was a function to take an unbalanced binary tree and make it balanced.
Let's define a new term, a faux-balanced tree. A tree with the same number of elements (plus or minus 1) on the left and right sides. This isn't the same as a truly balanced tree, which says that the deepest end of the tree and the shallowest end shouldn't be more than 1 level apart. All truly balanced trees are faux-balanced, but not all faux-balanced trees are truly balanced.
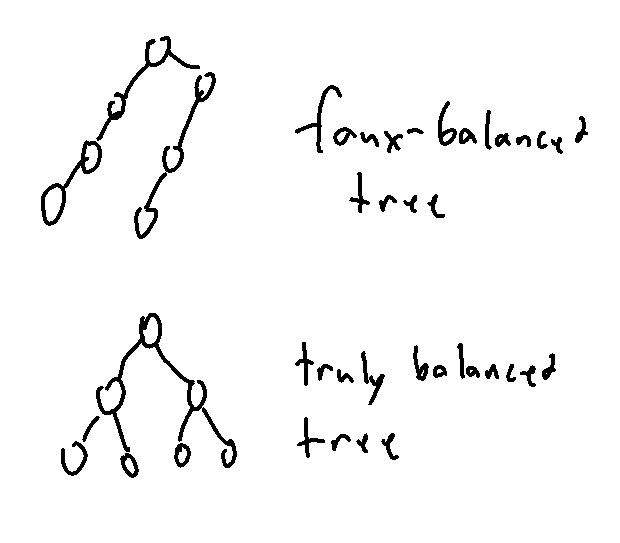
If every single node in a tree is faux-balanced, then the whole tree is truly balanced. This means that if we can get a single node faux-balanced, then faux-balance the children, we can truly balance an entire tree. The implication of this is that if we are able to move a single node from one side of a tree to the other, we can balance a binary search tree. This does, however, mean that we have to change the root node, as there are always going to be a certain number of elements less than the root node, and a certain number of elements greater than the root node, and we can't change either of those numbers without either changing the list, or changing the root node itself.
Just focusing on moving a node from the left side of a tree to the right side, we have to remove a node from the left side, replace the root node, and add to the right side. The only possible contender for the new root node is the largest node on the left side, the only possible contender for the node to remove from the left side is the new root that we just removed, and the only contender for the new node on the right side is the old root node.
This leads to our final algorithm:
- Take the largest node to the left of the root node and remove it
- Take the root node and add it to the right side of the root node
- Replace the root node with the node on the left side that you just removed.
This allows us to move a node from one side of a binary search tree to the other without breaking it, which allows us to create a faux-balanced tree, which allows us to create a balanced tree with recursion.
Addendum: I was very tired when I wrote this, it is terribly written. I think the information is correct and clear, but some things have to be clarified. First of all, this algorithm is designed to use O(1) memory, but takes O(n log n) time to execute. There are also better algorithms for self balancing trees. Rereading this I would really like to delete this, but it feels wrong to do so for some reason.